Mesurer l'aire sous une hyperbole en première S

André Stoll - IREM de Strasbourg –

  C'est en termes d'obstacles qu'il faut poser le problème de la connaissance scientifique […]
Toute connaissance est une réponse à une question.
S'il n'y a pas eu de question, il ne peut y avoir connaissance scientifique.

Bachelard, La formation de l'esprit scientifique, Vrin, 1938

Le problème de la mesure de l'aire sous une hyperbole que j'ai proposé à ma classe de première S sous forme de question ouverte, ne devait être au départ qu'une activité pour préparer les élèves à deux chapitres fondamentaux de la classe de terminale (le calcul intégral et la fonction logarithme). Vue les réactions des élèves, cette activité se révèlera beaucoup plus riche, m'amenant ainsi à introduire très naturellement d'autres outils comme la méthode d'Euler ou encore à leurs parler de la méthode des indivisibles, méthode (presque) complètement oubliée actuellement.

Les différents épisodes se sont déroulés au lycée Louis Couffignal de Strasbourg entre les mois de mars et juin. Lorsqu'il a été créé, ce lycée était « le lycée technique de Strasbourg ». Il n'a jamais été intégré dans la carte scolaire. Et on va au lycée Couffignal par choix ou parce qu' « on n'est pas bon en français (par exemple) ». Depuis peu, il accueille quelques élèves qui ont choisi l'option SVT mais la plupart des élèves suit l'option SI (sciences de l'ingénieur).

Acte I : Où on cherche à résoudre « un problème qu'on sait pas faire et que personne nous a jamais montré ».

 Le décor  : une salle de classe, neuf ordinateurs sur autant de tables, un rétroprojecteur sur une dixième table, des chaises, un tableau blanc.

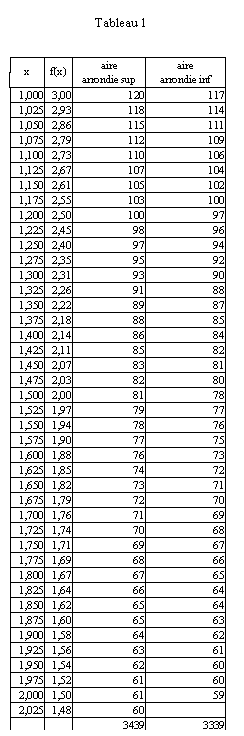
Scène 1  : Seize élèves entrent dans la salle où les attend le professeur. Ils s'installent, deux par ordinateur qu'ils allument machinalement. Le professeur allume le rétroprojecteur. Sur le mur, à côté du tableau blanc, apparaît la figure suivante (voir Figure 1 ) :

Le professeur dit tout en écrivant au tableau : «  Soit f la fonction définie sur l'intervalle par  et G la représentation graphique de f .

On défini alors la fonction A par :

où est l'aire de la surface délimitée par l'axe des abscisses, les droites d'équation , et la courbe G  .

Démontrer que : .  »

Après quelques instants, il rajoute : «  La courbe G est donnée. Il vous suffit de la récupérer sur mon ordinateur grâce au réseau. Je l'ai construite avec cabri-géomètre. Le fichier est appelé hyperbole.fig . L'unité de la figure est 4 cm ¹. »

Puis, il va s'asseoir, prend un livre et se met à lire.
Les élèves notent l'énoncé, ouvrent le fichier hyperbole.fig et se mettent à discuter, d'abord deux par deux puis par petits groupes, enfin tous ensemble.

Cherchent-ils la solution du problème posé ? Peut-être ou peut-être pas. Toujours est-il que ce temps de non-intervention du professeur est indispensable pour s'imprégner du problème mais aussi y réfléchir ².
Une dizaine de minutes plus tard, le professeur se lève. «  Qu'avez-vous trouvé ?  » dit-il.
Silence.
Il insiste. «  Vous avez probablement une idée ?  »

Nouveau silence.

• Marie intervient : «  Monsieur, ça ne marche pas votre truc !  »
• Le professeur : «  Et pourquoi ?  »
• Marie : «  A n'est pas une fonction !  »
• Le professeur, visiblement surpris par cette réponse : «  euh… je ne comprends pas ta remarque  »
• Marie : «  Ben oui, j'arrive pas à la mettre dans ma calculatrice donc ce n'est pas une fonction  »

Et cinq ou six élèvent approuvent Marie. ³
Christian : «  Et de toutes façons, comme deux plus trois font cinq, il doit y avoir une erreur dans l'énoncé  »

Le professeur, de plus en plus perplexe : «  C'est mal parti  » se dit-il tout bas puis pour les élèves « Je note ces questions et nous y reviendrons ultérieurement. En attendant, essayez de calculer les trois aires  »
Julien : «  Monsieur, j'ai une idée. On pourrait faire comme au primaire. En CM 2 la maîtresse nous a fait dessiner un cercle sur du papier millimétré puis elle nous a fait compter les petits carrés. On peut faire pareil ?  »
Le professeur, soulagé d'avoir enfin une réaction positive : «  Evidemment, et comme je n'ai pas de papier millimétré à portée de main, je vous imprime la courbe avec le logiciel Sine Qua non ⁴ »
Aussitôt dit, aussitôt fait et grâce à la simplicité de Sine Qua non , de l'imprimante et de la photocopieuse qui heureusement se trouve dans la salle à côté, en cinq minutes chaque élève dispose de la figure suivante :

Et chacun de se lancer dans le comptage des millimètres carrés avec enthousiasme (Ah qu'il était bien le temps de l'école primaire, de la maîtresse, unique, qu'on va encore voir parfois pour lui raconter les soucis lycéens quotidiens.)

Trois minutes passent peut-être quatre. L'enthousiasme retombe aussi vite qu'il était monté, car évidemment le comptage s'avère rapidement pénible et ennuyeux. Et puis, il y a les carrés qu' «  on sait pas comment faire parce qu'ils sont coupés par la courbe  » ; «  Faut-il les compter ou non ?  »
Pourtant Marie et sa voisine Julie persévèrent.
Christian avec son double décimètre mesure des hauteurs qu'il dicte à Jonas qui note consciencieusement :
A 0, on a 120 mm, à 5, on en a 105 mm puis à 10, 95 mm, à 15, 87 mm, à 20, 79 mm, à 25, 73 mm, à 30, 68 mm, à 35, 63 mm et enfin à 40, on en a 60.
Et après, une discussion animée :

• Entre 0 et 5 mm, il y a à peu prés 560 mm²
• Entre 5 et 10 mm, il y a à peu prés 500 mm²
• Entre 10 et 15 mm, il y a à peu prés 455 mm²
• Entre 15 et 20 mm, il y a à peu prés 415 mm²
• Entre 20 et 25 mm, il y a à peu prés 380 mm²
• Entre 25 et 30 mm, il y a à peu prés 352 mm²
• Entre 30 et 35 mm, il y a à peu prés 325 mm²
• Entre 35 et 40 mm, il y a à peu prés 300 mm²

Puis, ils additionnent et fièrement proclament leur résultat : «   » 5 Réaction immédiate de Kevin : «  C'est pas possible ! Comment t'as fait pour trouver un truc pareil ? Nous on s'embrouille » Timothée, celui qu'on n'entend jamais ou presque : «  Monsieur, on peut utiliser le tableur ?  » Le professeur : «  Bien sûr  » Il s'approche de la table de Timothée et Arnaud et essaie de comprendre leur démarche. Voici leurs explications (voir Tableau 1 ): «  Dans la première colonne, on a mis x. Comme 40 mm représente une unité, 1 mm représente unité. Il suffit alors d'écrire 1 dans la ligne 2 puis la formule dans la ligne suivante et de la tirer vers le bas jusqu'à obtenir 2. La colonne 2, c'est facile : On calcule . Les deux colonnes suivantes, on utilise les fonctions =ARRONDI.SUP(B4*40;0) et =ARRONDI.INF(B4*40;0) en multipliant d'abord la colonne 2 par 40 pour avoir des millimètres.  » «  Et le résultat ?  », demande le professeur Timothée : «  Il suffit d'additionner la colonne et on trouve  » Le professeur : «  Et  ? » Timothée : «  On refait la même chose mais on commence à 2 » Le professeur : «  C'est à dire ?  » Timothée : «  Pour trouver , on ajoute la portion de surface comprise entre 2 et 3 à  » Cette remarque étant évidente pour tous, le professeur va au tableau et propose d'introduire la notation suivante : «  On note . est donc l'aire de la surface définie par et en particulier, lorsque ,    »

Tous se remettent au travail et, avec plus ou moins de difficultés, arrivent aux résultats ci-dessous.
Pour ceux qui ont utilisé la méthode de Timothée et Arnaud :

D'où, ils ont déduit que :

Pour les autres :

, ,

D'où :

Et tous à la fois fiers d'avoir trouvé quelque chose et déçus parce que ce n'est pas ce qu'il fallait trouver, de conclure :
«  Il se pourrait que le résultat soit vrai  ».

Avant de quitter la salle, le professeur leur demande de réfléchir pour une prochaine séance à une méthode pour améliorer les résultats trouvés.

Scène 2  : Le professeur reste seul, en profite pour souffler quelques instants puis quitte à son tour la salle.

Scène 3  : Dans la même salle avec 16 autres élèves qui réagissent à quelques détails près de la même manière.

Sauf Philippe, le spécialiste de cabri-géomètre : «  Monsieur, en seconde, avec mon prof de maths, on a fait un travail sur les aires avec cabri. J'me souviens plus bien mais est-ce que je peux essayer de retrouver ?  »
Le professeur : «  Evidemment  »
Très vite, il revient à la charge : «  Ca ne va pas, car cabri ne calcule que l'aire des polygones  »
Le professeur en s'adressant à Philippe et à son voisin Matthieu : «  Faites comme Archimède ! Vous vous souvenez, on a vu lors d'un TD comment Archimède a démontré que l'aire d'un cercle est la même que l'aire d'un triangle rectangle de base le périmètre et de hauteur le rayon du cercle…  »
Le professeur n'a pas le temps de finir sa phrase que Philippe et Matthieu se lancent dans la construction suivante (voir Figure 3 )

Figure 3

Puis à l'aide de l'outil calculatrice de Cabri, ils trouvent :

, , et

Ils se satisferont de ces résultats malgré l'insistance du professeur qui montre sa déception devant le refus des deux élèves. «  Bof, il suffirait de prendre quelques points intermédiaires surtout entre 1 et 2 mais comme de toute façon on ne trouvera jamais de valeur exacte, ça ne sert à rien  » dit Matthieu .
Et avant de partir déjeuner, le professeur fait le point et les élèves conjecturent que  :

.

Scène 4  : Le lendemain, dans les couloirs, Thomas B., dont le père est ingénieur en génie civil, croise le professeur

 « Mon Père m'a dit que et que  . Donc si je prends et , je trouve :

et la proposition est démontrée.  »

Le professeur : «  Thomas, ton Père a bien sûr raison. Mais, sais-tu définir  ?  »

Thomas n'insiste pas et va rejoindre ses camarades.

Quelques jours plus tard :

Acte II : Où on calcule la dérivée de la fonction A

Dans une salle de classe du troisième étage, le professeur distribue aux 32 élèves de la classe « le sujet du devoir maison à faire pour la semaine suivante ».

Devoir numéro 8, à remettre mercredi 5 avril

Conseil avant de commencer le devoir  : revoir la définition du nombre dérivée d'une fonction f en .

Soit f la fonction définie sur l'intervalle par   et G la représentation graphique de f .

On définit alors la fonction A par :

où est l'aire de la surface délimitée par l'axe des abscisses, les droites d'équation , et la courbe G  . .

1. Dans cette question, on prend . h est un nombre réel. On appelle M le point de coordonnées et P le point de coordonnées
2. On suppose h positif.
3. Justifier les inégalités suivantes (pour les notations, voir la figure ci-dessus) :
   
   
   
4. On prend à présent h négatif. Montrer que dans ce cas :
   
   (indication : poser )
5. Déduire des inégalités et que la fonction A est dérivable en 2 et calculer
6. Généraliser le raisonnement pour quelconque.
7. Conclusion : énoncer le résultat sous forme de théorème.

Acte III : Où on trace la représentation graphique de la fonction A .

Deux semaines plus tard, les élèves ont fait leur devoir. Le professeur a corrigé les copies. On est de retour dans la salle informatique.

Le professeur rend les copies qui sont « bonnes » sauf la démonstration de l'inégalité ⁶. Et tous sont arrivés – plus ou moins personnellement - à la conclusion que A est dérivable et que ⁷

Le professeur : «  Souvenez-vous qu'au mois de décembre, dans le chapitre dérivée, nous avons parlé d'approximation affine d'une fonction. Nous avons traité l'exercice suivant : Soit f une fonction dérivable telle que : , , , . Calculez une valeur approchée de  »

Et tous de feuilleter leur classeur à la recherche de cet exercice qui est évidemment introuvable ainsi que l'approximation affine d'une fonction.

Le professeur : «  Je vous rappelle que l'approximation affine d'une fonction consiste à identifier au voisinage du point A de coordonnées la représentation graphique (C) de la fonction avec la tangente à (C) en A  »

Aucune réaction des élèves.

Le professeur : «  Quelle est l'équation de (C) ?  »

Presque tous : 

Le professeur : «  Et l'équation de la tangente ? »

Quelques uns : 

Le professeur : «  En prenant où h est un nombre petit… »

Il n'a pas le temps de finir sa phrase qu'on entend «   »

Et les calculatrices toujours aussi impatientes de se mettre à calculer.

Le professeur passe dans les rangs et compte : «  Une bonne réponse, deux, …, six  ». Il s'installe entre Marie et Julie et les aide à écrire les calculs : 

puis de même «   » et finalement Julie, fièrement d'annoncer «   ».

Pendant ce temps, les deux spécialistes du tableur ⁸, Timothée et Arnaud ont trouvé :

Arnaud explique ce tableau à ses camarades et essaie d'appliquer la méthode à la fonction A .
A part Christian et Alexandre qui s'énervent avec leur ordinateur qui refuse obstinément de démarrer, tous se mettent au travail et très vite apparaissent les premières courbes, représentations graphiques (approchées !) de A qui mérite enfin pour tous d'être classé dans la catégorie des fonctions !

Evidemment, dans l'exercice traité en classe et rappelé ci-dessus, le pas est . Donc, sans même réfléchir, tous ont pris comme pas .
Le professeur : «  Est il clair pour tous que ce n'est qu'une approximation de la représentation graphique de la fonction A  ? Comment pourrait-on trouver une meilleure approximation ?  »
Après quelques instants d'hésitation, Philippe qui ne se manifeste que lorsque les autres ne trouvent pas : «  Ben, il suffit de prendre deux valeurs successives de x plus proches  »
Le professeur : «  C'est à dire ?  »
Philippe : «  Ben, on a pris 0,1 entre deux valeurs de x. On pourrait essayer la moitié  »
Personne n'a écouté la réponse de Philippe et déjà, on essaie ou voire . Non, cette dernière valeur ne fonctionne pas car le nombre de lignes de calcul est vraiment trop grand.
On obtient ainsi les résultats suivants – après avoir multiplié par 1600 pour avoir les aires en mm²  :

A la fin de l'acte III, tous les élèves sont convaincus que A est une fonction, que la proposition est vraie et surtout que quelque soit la façon d'aborder le problème il faudra un moment donné faire intervenir une limite vers l'infini.
Le professeur : «  La méthode que vous avez utilisée pour représenter graphiquement A est appelée la méthode d'Euler, du nom de celui qui l'a trouvée. C'est certainement la première fois que vous entendez parler de Euler. Qui accepte de faire un exposé sur Euler ? »
Thomas L., qui a déjà fait un exposé sur Pythagore et Archimède, accepte ce nouvel exposé.

Acte IV : Où l'on démontre enfin que

Figure 5

L'acte IV se déroule dans la salle du troisième étage. Les 32 élèves sont présents.

Sans difficulté, on montre que l'égalité est équivalente à qui est elle même équivalente à l'égalité : .

Le professeur : «  Pour démontrer cette dernière égalité, on utilise une méthode inventée au début du dix-septième siècle par Cavalieri (1598-1647), un élève de Galilée. Pour comparer les aires de deux surfaces, on coupe celles-ci par des droites parallèles et on compare les segments ainsi obtenus. Cavalieri appelle ces segments des indivisibles. Il dit que lorsque deux surfaces sont formées des mêmes indivisibles alors ces deux surfaces ont la même aire.  » 

«  Par exemple (voir figure 6 ) pour montrer que la diagonale AC coupe le parallélogramme ABCD en deux triangles de même aire, on compare les indivisibles suivant la droite (AB). A chaque indivisible MN du triangle ACD correspond exactement un indivisible du triangle PQ du triangle ABC. D'où le résultat.  »

«  Un autre exemple que chacun traitera tout seul (voir figure 7 ):

A, B, C,…, J sont alignés. Sur une droite parallèle on prend les points M, N, P et Q. On suppose :

Alors les triangles ABM, CDN, EFP, GHQ et IJQ ont même aire.  »

«  Ou encore, comparons l'aire de l'ellipse E de grand axe a et de petit axe b à l'aire du cercle C de rayon a (voir figure 8 ). A tout indivisible MN de E correspond un indivisible PQ de C tel que . La méthode des indivisibles nous donne dans ce cas : et comme on a :

«  Pourtant, très rapidement, les géomètres se rendent comptent que cette méthode conduit à des résultats faux.  »

«  Par exemple (voir figure 9 ) :

Figure 9

A chaque indivisible MN suivant la base (CB) du triangle ABC correspond exactement un indivisible PQ du triangle DEF. Pourtant les deux triangles n'ont pas la même aire !  » 

«  Evidemment, la logique voudrait qu'on abandonne cette méthode puisqu'elle conduit à des résultats erronés »

Les élèves sont attentifs. D'habitude au bout de quelques minutes, ils ont un besoin urgent de communiquer avec leur voisin. Leur silence est presque gênant.

Le professeur continue :

«  Pourtant, Evangelista Torricelli (1608-1647) celui qui a donné son nom au baromètre, au lieu d'abandonner la méthode, fait une liste de situations paradoxales et en arrive à la conclusion qu'il existe des indivisibles plus ou moins épais ! Il considère les indivisibles, non pas comme des lignes mais comme des vestiges de surfaces petites et par suite, à attribuer une certaine épaisseur aux indivisibles  ».

«  Voici sur l'exemple précédent, le raisonnement de Torricelli :
Reprenons les deux triangles de la figure 9 Prenons M'N' un autre indivisible du triangle ABC et P'Q' l'indivisible correspondant du triangle DEF (voir figure 10 ). Alors: où h et k sont les longueurs des hauteurs des deux triangles ABC et DEF. Lorsque le point M' se rapproche du point M, le rapport ne dépend pas de H'. C'est donc tout naturellement que nous attribuerons cette valeur au rapport des épaisseurs des deux lignes MN et PQ. Notons e l'épaisseur de la ligne MN et e' celle de la ligne PQ, alors: et et finalement, on retrouve le résultat suivant bien connu :   » 

«  Appliquons à présent la méthode des indivisibles à notre problème. »

La surface ACDB est l'ensemble des indivisibles   MN où et lorsque . A chaque indivisible MN de ACDB on associe l'indivisible M'N' de la surface A'C'D'B' où et . Je dis que les indivisibles MN et M'N' ont même aire. Pourquoi ?  » 

Il s'arrête. Quelques doigts se lèvent.

Jonathan : «  Parce que les longueurs horizontales sont multipliées par 3 et les longueurs verticales sont divisées par 3 donc les aires ne changent pas !  »

Le professeur : «  Comme les deux aires ACDB et A'C'D'B' sont formées des mêmes indivisibles, leurs aires sont égales et notre égalité est démontrée  »

Cette dernière phrase prononcée, la classe qui semblait endormie se réveille. Les élèves ressentent le besoin de bouger, de remuer, de parler…comme après un devoir en classe.

Acte V : Où l'on cherche à prolonger la fonction A

Deux ou peut être trois semaines plus tard, on est de retour dans la salle informatique. Les élèves entrent dans la salle. Curieusement les ordinateurs restent éteints…

• Le professeur : «  Récapitulons rapidement les propriétés de la fonction A  »
• Julien : «  La définition, c'est l'aire d'une surface  »
• Le professeur : « D'accord mais essaie d'être plus précis »
• Et Julien d'essayer d'être plus précis.
• Christian : «  Elle est dérivable et sa dérivée est   et »
• Et le professeur écrit ces deux propriétés au tableau. 
• Le professeur : «  Est-il possible de généraliser cette dernière égalité ? »
• Cyril : « On pourrait par exemple écrire  »
• Le professeur : «  Que représentent a et b dans cette égalité ?  »
• Cyril : «  Deux nombres quelconques  »
• Le professeur : «  Deux nombres quelconques ?  »
• Cyril : «  J'ai oublié, il faut les prendre plus grands que 1 »
• Le professeur : «  D'accord, et pour gagner un peu de temps   nous admettrons cette propriété dans le cas général »

Et le professeur écrit au tableau : 

Théorème

(Démontré dans le cas particulier , , admis dans le cas général)

Lorsque a et b sont deux nombres réels supérieurs à 1, alors

Le professeur :«  Jusqu'à présent nous nous sommes limités à . Or la fonction f définie par qui a engendré la fonction A est définie pour . Est-il possible de définir A pour  ? »

C'est bientôt la fin de l'année scolaire. Les élèves (enfin presque tous c'est à dire environ les ¾ de la classe) ont fini par comprendre qu'un temps de recherche est nécessaire.

Un quart d'heure passe. Le professeur passe de table en table. Marie qui est associée à Julien propose : « tout simplement on reprend la définition de A que vous nous avez donnée il y a longtemps  » Le professeur : «  c'est-à-dire   ?  » Marie et Julien en même temps «  l'aire de AMNB  » et ils montrent le dessin ci contre qu'ils ont griffonné sur une feuille. Le professeur : «  D'accord si on définit A de cette manière. Que peut-on dire du sens de variation de la fonction A ?  » Après un temps de réflexion et de discussion, où on entend : «  Quand M s'approche de zéro, l'aire diminue donc elle est décroissante  » Le professeur : «  Dans ce cas une des propriétés de A n'est plus vraie. Voyez-vous laquelle ?  » Puis «  Réfléchissez et essayez de modifier votre définition en conséquence. Je reviens vous voir dans quelques instants  »

Timothée et Arnaud ont tout naturellement pensé à la méthode d'Euler : «  On est parti de qui est valable lorsque a est plus petit que 1 et on a appliqué la méthode que vous nous avez donnée et avec le tableur on a dessiné la courbe. »

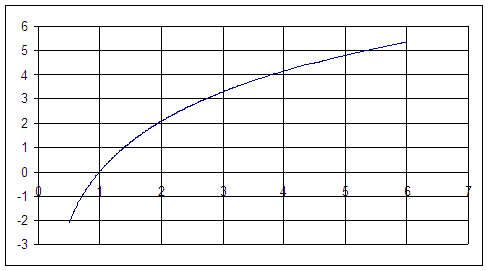
Le professeur : «  Initialement, A représente une aire. Or d'après votre graphique est négatif lorsque a est compris entre 0 et 1. Qu'en pensez vous ? »

Quand le professeur vient les voir, Philippe et Kevin proposent : «  On a pris a entre 0 et 1. Alors est plus grand que 1 et on a écrit : . Comme on connaît alors et le tour est joué »

Le professeur : «  Que devient la dérivée de la fonction A dans cas ?  »

Le professeur s'approche du tableau: «  Faisons la synthèse de vos découvertes  ».

Il partage le tableau en trois parties et expose les résultats trouvés. En voyant le résultat de Timothée et Arnaud, Marie et Julien acceptent l'idée d' «  une aire négative parce qu'elle est décrite dans le sens trigonométrique alors que quand on la décrit dans le sens des aiguilles d'une montre elle est positive ou l'inverse »

Quant à Philippe et Kevin : «  Puisque A est l'opposée de l'aire, on peut faire comme dans le devoir maison et montrer que ça marche »

Le professeur : « Je vous propose d'anticiper sur le programme de terminale et de généraliser la formule

Il énonce le théorème de dérivation des fonctions composées et demande aux élèves de l'appliquer au résultat de Philippe et Kevin  c'est à dire lorsqu'on pose :

et évidemment on retrouve le point de départ de Timothée et Arnaud :

Les différentes approches de ce dernier problème de l'année scolaire sont valables !

Deux (ou peut être trois) ans plus tard dans une classe de BTS

Le même professeur : «  Voici un exemple de calcul d'une intégrale par changement de variable. Représentez graphiquement la fonction f définie sur l'intervalle par puis calculez l'aire délimitée par la représentation graphique de f et l'axe des abscisses. On pourra poser  »

Quelques secondes plus tard, Christian (le même que ci-dessus, certes beaucoup plus grand et plus chevelu) se lève et dit : «  Monsieur c'est facile la représentation graphique de f est une ellipse parce que si je l'étire dans le sens des y de quatre tiers je trouve un cercle et les indivisibles que il y a quelques années vous nous avez montrés disent que dans ce cas l'aire est multipliée par quatre tiers et que l'aire du cercle est pi fois r au carré alors je fais 16pi sur deux parce que ce n'est qu'un demi cercle et je divise par quatre et je multiplie par trois et finalement ça fait que l'intégrale vaut six pi et j'ai pas besoin de changement de variable  »

• 1 Pour des raisons de mise en page, cette unité n'a pas été respectée dans les figures de l'article.
• 2 Les premières fois les élèves sont surpris de cette réaction. Ils ont tellement pris l'habitude dans leur scolarité d'être guidés qu'à la moindre difficulté ils s'arrêtent et attendent des indications.
• 3 En fait, cette réaction n'est nullement surprenante puisque la notion de fonction est introduite en troisième et en seconde à partir d'exemples où il s'agit de faire du calcul. Quand les élèves arrivent en 1S  on  estime que la notion est acquise alors que celle-ci n'a (presque) jamais été définie (même pas approximativement).
  Il y a d'autres exemples du même type dans l'enseignement des mathématiques : l'ensemble des nombres réels, la notion de limites,... Bien sûr, il n'est pas possible, ni souhaitable, dans le cadre de l'enseignement secondaire, de se lancer dans des théories que les élèves auraient du mal à comprendre. A condition d'en accepter les conséquences
• 4Sine Qua non est un traceur de courbes bien sympathique. On peut le télécharger gratuitement à l'adresse suivante : ( http://perso.orange.fr/patrice.rabiller/SineQuaNon/menusqn.htm )
• Merci à son concepteur
• 5 En fait ce n'est que plus tard que j'ai compris leur méthode. Comme la mesure de mm en mm s'avère difficile, voire impossible, ils ont mesuré les hauteurs de 5 mm en 5 mm puis ils ont fait la moyenne des deux longueurs et ont multiplié par 5. Ce qui revient – sans qu'ils s'en rendent compte et moi non plus sur le coup - à calculer l'aire des trapèzes.
  Très souvent, lorsque les élèves travaillent de cette manière, il faudrait avoir le don d'ubiquité, arriver à décoder instantanément leur problématique qu'ils expriment dans un langage « crypté » et comprendre leurs méthodes. Et parfois, je passe à côté de solutions sur lesquelles il faudrait rebondir. Il arrive aussi qu'il y ait quelque erreur que l'on ne détecte pas immédiatement comme c'est le cas dans la solution proposée par Timothée et Arnaud.
• 6 Décidément, il n'y a rien à faire « devant h, il y a un signe +, donc h est un nombre positif ! »
• 7 Curieusement, pour quelques élèves A n'est toujours pas une fonction ! Et pourtant A est dérivable.
• 8 Le tableur est utilisé fréquemment en SI. Les élèves qui ont choisi cette option en seconde manipulent tous cet outil avec beaucoup de facilités.